Python x 알고리즘 : 스택, 큐, 재귀함수 등
2023. 8. 7. 16:32ㆍ[알고리즘]/Algorithm
꼭 필요한 자료구조 기초
탐색
- 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 의미
- 그래프, 트리 등의 자료구조 안에서 탐색을 하는 문제를 주로 다룸.
- 대표적인 탐색 알고리즘으로 DFS와 BFS가 있다.
자료구조
- 데이터를 표현하고 관리하고 처리하기 위한 구조를 의미
- 그 중 스택과 큐는 자료구조의 기초 개념으로 두 핵심적인 함수로 구성된다.
- 삽입(Push) : 데이터를 삽입한다
- 삭제(Pop) : 데이터를 삭제한다.
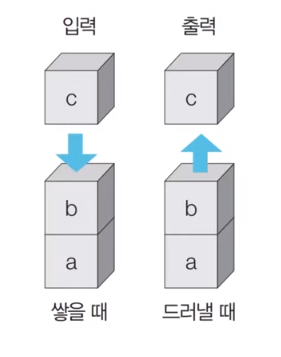
🍃 스택(Stack)
- 스택은 박스 쌓기에 비유할 수 있다.
- 선입후출(First In Last Out) 구조 또는 후입 선출(Last In First Out) 구조라고 한다.
- 파이썬에서 스택은 별도의 라이브러리를 사용할 필요가 없다. 기본 리스트에서 append()와 pop() 메서드를 이용하면 된다.
# 스택 파이썬 구현
stack = []
# 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
stack.append(5) # 5
stack.append(2) # 5 2
stack.append(3) # 5 2 3
stack.append(7) # 5 2 3 7
stack.pop() # 5 2 3
stack.append(1) # 5 2 3 1
stack.append(4) # 5 2 3 1 4
stack.pop() # 5 2 3 1
print(stack) # 최하단 원소부터 출력 - 5 2 3 1
print(stack[::-1]) # 최상단 원소부터 출력 - 1 3 2 5
🍃 큐(Queue)
- 큐는 대기줄에 비유할 수 있다.
- 나중에 온 사람일수록 나중에 들어가기 때문에 흔히 "공정한" 자료구조라고 비유된다.
- 선입선출(First In First Out) 구조라 한다.

from collections import deque
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque()
# 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
queue.append(5) # 5
queue.append(2) # 2 5
queue.append(3) # 3 2 5
queue.append(7) # 7 3 2 5
queue.popleft() # 7 3 2
queue.append(1) # 1 7 3 2
queue.append(4) # 4 1 7 3 2
queue.popleft() # 4 1 7 3
print(queue) # 먼저 들어온 순서대로 출력 - 3 7 4 1
queue.reverse() # 다음 출력을 위해 역순으로 바꾸기
print(queue) # 나중에 들어온 원소부터 출력 - 4 1 7 3
🍃 재귀함수(Recursive Function)
- 재귀함수란 자기 자신을 다시 호출하는 함수를 의미한다.
- 무한한 재귀 호출을 진행할 수 없다.(재귀의 최대 깊이를 초과하면 에러가 발생한다.)
- 따라서 꼭 종료 조건!!을 설정해주어야 한다.
def recursive_function():
print('재귀 함수를 호출합니다.')
recursive_function()
recursive_function()
#예전에 공부했을 때 종료 조건이 있어야 무한 반복을 멈출 수 있다.- 재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수가 언제 끝날지, 종료 조건을 꼭 명시해야 한다.
- 종료 조건을 명시하지 않으면 함수가 무한 호출될 수 있다.
def recursive_function(i):
# 100번째 호출을 했을 때 종료되도록 종료 조건 명시
if i== 100:
return
print(i, '번째 재귀함수에서', i + 1, '번째 재귀함수를 호출합니다')
recursive_function(i + 1)
print(i, '번째 재귀함수를 종료합니다')
recursive_function(1)이 코드에서 if i == 100은 종료 조건이다.
재귀 함수를 한번 돌릴 때마다 자기 자신에 i + 1를 넣어 다시 호출해주고 조건이 맞을 때 까지 호출을 반복하게 된다.
- 재귀 함수를 이용하는 대표적 예제로는 팩토리얼 문제가 있다.
# 반복적으로 구현한 n!
def factorial_iterative(n):
result = 1
# 1부터 n까지의 수를 차례대로 곱하기
for i in range(1, n + 1):
result *= i
return result
# 재귀적으로 구현한 n!
def factorial_recursive(n):
if n <= 1: # n이 1 이하인 경우 1을 반환
return 1
# n! = n * (n - 1)!를 그대로 코드로 작성하기
return n * factorial_recursive(n - 1)
# 각각의 방식으로 구현한 n! 출력(n = 5)
print('반복적으로 구현:', factorial_iterative(5))
print('재귀적으로 구현:', factorial_recursive(5))
반응형
'[알고리즘] > Algorithm' 카테고리의 다른 글
| Python x 알고리즘 : 정렬 (0) | 2023.08.09 |
|---|---|
| Python x 알고리즘 : 탐색 알고리즘 DFS/BFS (0) | 2023.08.07 |
| Python x 알고리즘 : 구현(Implementation) (0) | 2023.08.04 |
| Python x 알고리즘 : 복잡도 (0) | 2023.08.03 |
| 코딩 테스트 사이트 모음 (0) | 2023.04.26 |